Potential ET - PM - ESAT - SWPE - SWGE - SWGRA - CANOPY - ROUGH - SRSC - FRSS - WEATHER - WNDADJ
July 10, 2015
In this section, most equations are given in standard algebraic notation, as extended by Shuttleworth and Wallace (1985). The correspondence between algebraic notation and variable names is:
| rsc | RSC | za | ZA | Rn | RN | Δ | DELTA |
| raa | RAA | d | DISP | R | SOLRAD | gsc | GSC |
| rac | RAC | dc | DISPC | A | AA | Lp | LAI |
| ras | RAS | z0 | Z0 | As | ASUBS | Sp | SAI |
| rss | RSS | z0c | Z0C | Da | VPD | fT | FT |
| Cc | CC | h | HEIGHT | D0 | D0 | fD | FD |
| Cs | CS | u* | USTAR | ea* | ES | R0 | R0 |
| Mc | PMC | Kh | KH | ea | EA | Ra | RA |
| Ms | PMS | uh | UH | Ta | TA | Rs | RS |
| Rc | RC | zb | HIBL | ua | UA | uw | UW |
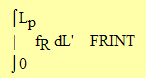
and for the parameters and constants is:
| T1 | T1 | glmin | GLMIN | n | NN | Lvρw | 1/ETOM |
| T2 | T2 | glmax | GLMAX | z0g | Z0G | cpρ | CPRHO |
| TL | TL | cD | CVPD | w | LWIDTH | γ | GAMMA |
| TH | TH | Rm | RM | ρtp | RHOTP | k | K |
| F | FETCH | R.5 | R5 | Lpc | LPC | ||
| zw | ZW | cR | CR | ||||
| z0w | Z0W |
A common approach to estimating evaporation calculates a potential evaporation (PE) from weather variables, and then reduces actual evaporation below PE in response to soil drying. PE quantifies what the evaporation rate would be in the absence of any limitation of liquid water supply to the evaporating surfaces. It is thus an upper limit to the evaporation rate. Actual evaporation falls below the potential rate whenever liquid water supply to the plant leaves or to the soil surface cannot maintain the PE rate. Changing knowledge of limitations on evaporation has produced a variety of definitions of PE, which are related to the methods chosen to calculate it (Shuttleworth, 1991).
Federer et al. (1996) use the term "potential evaporation" (PE) as a generic term to include the general concept and all definitions and methods. Then they distinguish three fundamentally different definitions of PE by subscripts. Reference-surface PE (PEr) is defined as the evaporation that would occur from a specified or reference land surface in given weather conditions with soil water at field capacity (Shuttleworth, 1991); the reference surface is normally defined as a short, complete, green plant cover. Surface-dependent PE (PEs) is defined as the evaporation that would occur from any given land surface in given weather conditions if plant surfaces were externally dry and soil water was at field capacity. Potential interception (PEi) is defined as the evaporation that would occur from any given land surface in given weather conditions if all plant and soil surfaces were externally wetted, as by rain. PEi and PEs depend on surface characteristics, most notably on canopy height and stomatal resistance respectively.
Shuttleworth and Wallace (1985) applied the well-known Penman-Monteith equation separately for the canopy and for the soil surface to give separate estimates of transpiration and soil evaporation. The Shuttleworth-Wallace approach was designed to be applicable to canopies of any leaf area index or "sparseness". Federer and others (1996) developed the Shuttleworth-Wallace method to estimate PEs and PEi for any land surface. To obtain the potential soil evaporation component, they used a soil surface at field capacity for PEs and a saturated soil surface for PEi.
However, BROOK90 separates evaporation into two pathways and five processes controlled by five resistances to vapor transfer:
canopy evaporation
IRVP raa + rac evaporation of intercepted rain
ISVP raa + rac evaporation of intercepted snow
TRAN raa + rac + rsc transpiration
ground evaporation
SNVP raa + ras evaporation from snow on the ground
SLVP raa + ras + rss soil evaporation
where raa is the above canopy resistance, rac and ras are the within canopy resistances from the canopy and from the ground (soil/snow), rsc is the canopy surface resistance (predominantly stomatal resistance), and rss is the resistance to vapor movement within the soil. These are the five resistances in the Shuttleworth-Wallace equations.
In BROOK90 only one canopy process and one ground process can occur at any given time. For IRVP, ISVP, and SNVP, the evaporating surfaces are always assumed saturated when the processes are occurring. In other words, they always evaporate at their own potential rate. The output value PINT is the interception evaporation that would occur if the canopy were continually wetted by snow or rain. IRVP and ISVP are equal to PINT as long as intercepted rain or snow remain on the canopy. Snow interception is treated identically with rain interception, with no allowance for melting the intercepted snow. When there is no interception, BROOK90 calculates and outputs potential transpiration, PTRAN, which is the transpiration that would occur if stomatal opening were not restricted by water supply to the leaves. It then reduces transpiration below PTRAN if low water supply to the leaves causes stomatal closure. For SNVP, BROOK90 avoids or neglects numerous problems of snow energy balance and any interaction with canopy evaporation by using only the vapor gradient and raa + ras, effectively a potential rate (see SNO-SNOVAP).
Because the ground evaporation and the canopy evaporation are calculated simultaneously in the Shuttleworth-Wallace equations, the potential interception or transpiration depend on the value of rss (which is zero for snow or saturated soil). Potential conditions for the canopy processes often do not occur at the same time as potential conditions for the surface processes. When there is no snow on the ground, BROOK90 calculates potential canopy evaporation using the ambient soil resisistance, rss. When there is snow, BROOK90 calculates surface snow evaporation using raa + ras and the vapor gradient, and canopy evaporation using rss = 0. The equations then provide the soil (ground) evaporation (GER) corresponding to PTR and the soil evaporation (GIR) corresponding to PIR. If actual transpiration is less than PTR, soil evaporation is recalculated.
Theoretically the Penman-Monteith and Shuttleworth-Wallace equations are only valid for a short time period over which the weather variables are effectively constant. However, in spite of their non-linearities, the equations also give reasonable values when used with weather variables averaged over daily and even monthly periods (Federer et al. 1996). Although BROOK90 uses only daily weather data, PE estimates could be made for shorter time periods such as hourly by assuming diurnal distributions of weather variables. However, this would be costly of computer time. Tanner and Pelton (1960) suggested that the Penman equation would be more accurate when used on a daily basis if daytime and nighttime were separated. Federer et al. (1996) show that separation of daytime and nighttime also works well with the Shuttleworth-Wallace method.
BROOK90 obtains evaporation rates separately for daytime and nighttime within a day-night evaporation loop. All solar radiation (SOLRAD) is assigned to the daytime. The atmospheric humidity (EA) is assumed constant through the day ("day" refers to 24 hours). The daytime and nighttime values of air temperature and wind speed are obtained in subroutine WEATHER using function WNDADJ. Vapor pressure deficit (VPD) is obtained using subroutine ESAT. Subroutine CANOPY uses function INTERP to obtain canopy structure variables for the day. Subroutine ROUGH gets canopy roughness parameters. Within a day-night loop, the three aerodynamic resistances needed by the Shuttleworth-Wallace method are calculated in subroutine SWGRA. The canopy surface resistance (RSC) for the daytime is obtained from subroutine SRSC, and the soil surface resistance (RSS) in function FRSS. Subroutine SWPE uses function PM along with the various resistances to obtain potential transpiration rate (PTR) and the associated ground or soil evaporation rate (GER) by the Shuttleworth-Wallace equations. Subroutine SWPE is called again with RSC = 0 to give potential interception rate (PIR) and its associated soil evaporation rate (GIR). Subroutine TBYLAYER obtains actual transpiration by layer (ATRANI). If the actual transpiration is less than the potential, a new, higher GER is calculated by subroutine SWGE. BROOK90 then weights the daytime and nighttime rates by the solar daylength (DAYLEN) to obtain average rates for the day, PTRAN, GEVP, PINT, GIVP, and TRANI, which are used in later calculations.
In BROOK90, PEs (surface-dependent potential evapotranspiration) is not directly calculated, because that would involve changing the value of rss to its potential value (at field capacity), which would then change the values of IRVP, ISVP, and PTRAN. Can users obtain a value of PEs for comparison with other studies? In July 2013, in response to a query by Stefan Plötner, I have figured out how PEs can be obtained. BROOK90 must be run with two parameter changes:
These parameter changes may increase SLVP a lot, and will reduce PTRAN and ISVP a little,
but will not change ISVP and SNVP. An estimate of PEs can then be obtained as:
PEs = PTRAN + SLVP + IRVP + ISVP + SNVP.
The Penman-Monteith equation is
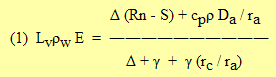
where E is the evaporation rate in volume of water per unit land area per unit time, Lv is the latent heat of vaporization for water, ρw is the density of water, Δ is the rate of change of vapor pressure with temperature, Rn is the net radiation above the surface, S is the subsurface heat flux, cp is the heat capacity of air, ρr is the density of air, Da is the vapor pressure deficit in the air, γ is the psychrometer constant, rc is the "canopy resistance", and ra is the aerodynamic resistance between the canopy and a reference height za at which Da is measured. The vapor pressure deficit, Da, is ea* - ea. The equation assumes that the vapor pressure at the effective evaporating surface, e0, is the saturated vapor pressure at the surface temperature. Then rc and ra are the two "resistances" through which water vapor passes as it moves down the vapor pressure gradient from e0 to ea. The canopy resistance, rc, represents resistance to flow of vapor through the stomates and cuticle of individual leaves and through the air around each leaf to some "effective" source height of water vapor in the plant canopy. The aerodynamic resistance, ra, is a measure of the turbulent transfer capability of the atmosphere between the effective source height and za. The Penman-Monteith equation is derived from the energy balance equation and the mass transfer equations for sensible and latent heat fluxes (e.g. Brutsaert 1982).
The subroutine ESAT calculates the saturated vapor pressure (kPa), e*, from temperature (°C), T , and calculates Δ. The equations of Murray (1967) are used. If T >= 0°C then
e* = 0.61078 exp[ 17.26939 T / ( T + 237.3 ) ]
Δ = 4098 e* / ( T + 237.3 )2
or if T < 0°C
e* = 0.61078 exp[ 21.87456 T / ( T + 265.5 ) ]
Δ = 5808 e* / ( T + 265.5 )2.
Shuttleworth and Wallace (1985) (SW) modified the Penman-Monteith method to account separately for the different water vapor and sensible heat pathways from the soil and from the leaves. Instead of the two resistances of equation (1), rc and ra, SW define five: rsc, raa, rac, ras, and rss. Resistances rsc and rac are in the transpiration pathway while rss and ras are in the soil evaporation pathway and raa is common to both. The canopy surface resistance, rsc, is the resistance to movement of water vapor out of the leaves. The resistance rac restricts vapor movement from the leaf surfaces to the effective source height for water vapor in the canopy. The resistance between the source height and a reference height above the canopy is raa, which corresponds to ra in equation (1). The reference height is that at which air temperature, humidity, and wind speed are known. The resistance to movement of water vapor from inside the soil to the soil surface is rss. The resistance to vapor movement from the soil surface to the source height is ras. The resistances rac, ras, and raa are assumed also to apply to sensible heat transfer.
Shuttleworth and Wallace (1985) start with
(2) Lv ρw E = Lv ρw Ec + Lv ρw Es
where Ec is transpiration and Es is soil evaporation, then write an equation similar to (1) for each term
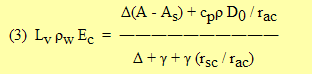
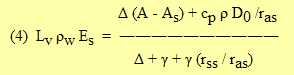
where D0 is the vapor pressure deficit at the effective source height, A is Rn - S or the available energy above the canopy, and As is Rns - S or the available energy at the ground. From the relationships of sensible and latent fluxes to the gradients and resistances, and using the definition of Δ, Shuttleworth and Wallace obtain
(5) D0 = Da + raa [Δ A - (Δ + γ) Lv ρw E ] / cpρ
Algebraic manipulation of (2), (3), and (4) to eliminate D0 leads to:
(6) Lv ρw E = Cc Mc + Cs Ms
where
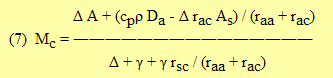
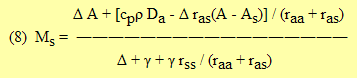
(9) Cc = 1 / { 1 + Rc Ra / [ Rs ( Rc + Ra ) ] }
(10) Cs = 1 / { 1 + Rs Ra / [ Rc ( Rs + Ra ) ] }
with
(11) Ra = (Δ + g) raa
(12) Rs = (Δ + γ) ras + γ rss
(13) Rc = (Δ + γ) rac + γ rsc
Although the algebra appears complicated, these equations for the first time provide a PM-type theory that includes both transpiration and soil evaporation. The total evaporation, E, must be obtained from (6) first, then D0 from (5), before the two components can be calculated from (3) and (4). Subroutine SWPE includes equations (3) through (13), more or less in reverse order.
The outputs Ec (PRATE) and Es (ERATE) from SWPE are in units of mm/d whereas Lvρw E in (1) is output as W m-2 from function PM. The conversion is ETOM * WTOMJ .
The Shuttleworth-Wallace approach incorporates the energy tradeoff between transpiration and soil evaporation. When transpiration is reduced by low availability of soil water or is zero, BROOK90 uses the new value of transpiration, Ec (ARATE), in subroutine SWGE to get a new value of soil evaporation, Es (ERATE). With Ec known, substituting(5) into (4) and (4) into (2) and solving for Lv ρw E gives
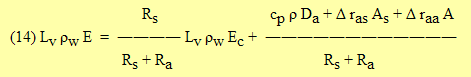
then
(15) Lv ρw Es = Lv ρw E - Lv ρw Ec
The three SW aerodynamic resistances, raa, ras, and rac are obtained in subroutine SWGRA by the methods of Shuttleworth and Gurney (1990). The derivations of their equations are not given here.
The friction velocity, u*, is first obtained from the classic logarithmic wind profile as
(16) u* = k ua / ln [ ( za - d ) / z0 ]
where ua is the wind speed at the reference height, za, z0 is the surface roughness parameter, d is the zero-plane displacement, and k is the von Karman constant. The roughness parameter is a measure of the turbulence-inducing properties of the surface. The zero-plane displacement, d, arises because the height of the effective canopy surface is above the ground surface that is taken as zero height. Both z0 and d are obtained in subroutine ROUGH . This u* equation strictly only applies for neutral atmospheric stability. Corrections for non-neutral stability are well-known (Brutsaert 1982), but are not usually considered where the objective is to evaluate PE for periods of a day and are not used in BROOK90.
Shuttleworth and Gurney (1990) assume that the classic logarithmic wind profile applies above the canopy and that an exponential profile applies within the canopy. As the canopy becomes sparser, they further assume that the effective source height of the energy fluxes remains at the same height as for a closed canopy, Dc = z0c + dc; these values are obtained in subroutine ROUGH. The ground to source height resistance, ras, is obtained by integrating the exponential eddy diffusivity from 0 to Dc to give
(17) ras = [ h exp(n) / n Kh] [exp( -n z0g / h ) - exp( -n Dc / h ) ]
and the source height to reference height resistance, raa, is obtained by integrating from Dc to za as
(18) raa = ln [ ( za - d ) / ( h - d ) ] / k u* + ( h / n Kh ) { -1 + exp[ n (h - Dc) / h ] }
where n is the extinction coefficient for eddy diffusivity, z0g is the roughness parameter of the underlying ground surface, and the eddy diffusivity at the canopy height, h, is
(19) Kh = k u* (h - d).
The exponential wind profile and the derived K(z) are known to be incorrect in canopies of intermediate leaf area index, but a better model is not yet available (Choudhury and Monteith 1988).
The leaf to zero plane resistance, rac, is assumed by Shuttleworth and Gurney (1990) to be a sum of the individual leaf laminar boundary layer conductances, so
(20) rac = ( n / ab ) ( w / uh )1/2 / { ρ tp Lp [ 1 - exp( -n / 2 ) ] }
where n is the extinction coefficient for eddy diffusivity, ab is a constant = 0.01 m/s0.5 (Campbell 1977), ρtp is the ratio of projected leaf area to total leaf surface area, Lp is the projected leaf area index, w is the representative leaf width in m, and uh is the wind speed in m/s at the top of the canopy. (Note that Shuttleworth and Gurney (1990) should have n in the numerator, not the denominator.) The rac equation strictly applies only to flat leaves and needles, not to cylindrical needles; but rac is small when w is small so this inaccuracy is negligible. The canopy-top wind speed, uh, is
(21) uh = (u* / k) ln [ ( h - d ) / z0 ].
In the Shuttleworth and Gurney equation, rac goes to infinity as Lp goes to zero, but this neglects the contribution of stems and branches to interception loss, especially when Lp = 0. Although the rac equation is specifically for leaves with width w, subroutine SWGRA uses (ρtp Lp + π Sp) for r tp Lp in equation (20), where Sp is the projected stem area index, defined analagous to Lp as the ratio of projected surface area of stems and branches to ground area (Federer et al. 1996). This assumes that a unit of stem surface has the same influence on rac as a unit of leaf surface. To avoid zero divides when Sp = 0, Lp is prevented from being less than 0.00001.
The Shuttleworth - Gurney separation of rac and rsc at the canopy level rather than at the leaf level is theoretically incorrect. In reality, the leaf boundary layer resistance and the leaf diffusion resistance are in series on each side of flat leaves (Jarvis and McNaughton 1986). The two resistances should be summed over each side of the leaf before integrating over the canopy, but this is too complicated for practical application (Choudhury and Monteith 1988).
Subroutine CANOPY calculates plant "parameters" that can vary with day of the year ( DOY).
The height of the canopy above any snowpack, h (HEIGHT), is
HEIGHT = RELHIT * MAXHT - SNODEP
where MAXHT is the maximum height for the year, which is an input parameter, and RELHIT is the relative height for the day of the year (doy), as obtained with function INTERP from the RELHT parameter array. HEIGHT is not allowed to be less than 0.01 m, which gives an appropriate roughness parameter for "smooth" surfaces. The snowpack depth (SNODEP, m) is the snow water content (SNOW, mm) divided by 1000 times snow density (SNODEN), which is assumed constant. Although snow density can actually vary from 0.05 to 0.5, the constant value is good enough to account for burying of the canopy in BROOK90. The RATIO of uncovered HEIGHT to total height (RELHT * MAXHT) is also calculated.
Actual projected leaf area index, Lp (LAI), is
LAI = MAXLAI * RELLAI(DOY) * DENSEF * RATIO
where MAXLAI is the maximum LAI for the year, RELLAI(DOY) is the relative LAI for the doy as obtained with function INTERP from the RELLAI parameter array, DENSEF is a thinning parameter between zero and one (see below). The use of RATIO assumes that LAI is distributed uniformly with height. LAI is prevented from being less than 0.00001 to avoid zero divides; this can cause small amounts of transpiration, which may be ignored.
Actual projected stem area index Sp (SAI), is assumed proportional to HEIGHT following Federer et al. (1996), so
SAI = CS * HEIGHT * DENSEF
where CS is a parameter that is the ratio of SAI to HEIGHT.
Total root length per unit area (RTLEN) is
RTLEN = MXRTLN * RELHT * DENSEF
where MXRTLN is the maximum root length for the year. Correction for seasonal RELHT assumes that root length increases proportionally with height growth.
The total plant resistance to water movement (RPLANT) is
RPLANT = 1 / (MXKPL * RELHT * DENSEF)
where MXKPL is the plant conductivity at maximum height growth. RPLANT is not allowed to be greater than 1E8 MPa d/mm, which is effectively infinite. Correction for seasonal RELHT assumes that canopy conductance increases proportionally with height growth.
DENSEF is normally 1.0 in the above four equations. This parameter was included in the model as a convenient way to "thin" a canopy by removing a fraction of the plants. LAI, SAI, and RTLEN are all reduced proportionally to DENSEF, and RPLANT is increased. However DENSEF does NOT reduce HEIGHT because the remaining canopy still has the same height. Therefore DENSEF should NOT be set to 0 to simulate a clearcut as HEIGHT is unchanged and the aerodynamic resistances will be wrong. Probably DENSEF should not be less than 0.05.
ROUGH obtains the roughness parameter, z0 , and the zero-plane displacement, d, based on canopy height, h, the projected leaf area index, Lp, and the projected stem area index, Sp. The methods used follow Shuttleworth and Gurney (1990) with some modifications. Shuttleworth and Gurney (1990) defined plant canopies as either "closed" or "sparse" based on whether Lp is greater or less than some arbitrary value Lpc, which they take as 4. Following Federer et al. (1996), BROOK90 defines a closed canopy as having Lp + Sp greater than Lpc + Spc, where Spc is taken as cs h, as described in the previous section. Spc is not reduced by DENSEF. RATIO is ( Lp + Sp ) / ( Lpc + Spc ) (this RATIO differs from RATIO in subroutine CANOPY). When RATIO is greater than or equal to 1, the canopy is "closed" and z0 and d are the values for a closed canopy.
The roughness parameter for closed canopies, z0c (Z0C), has been determined experimentally from wind profile data to be about 13% of h for relatively short canopies, but only 5% or less of h for some forests (Brutsaert 1982; Shuttleworth 1989). Following Federer et al. (1996) BROOK90 parameterizes the ratio z0c / h as follows: czs is the ratio for smooth surfaces with h less than hs; czr is the ratio for rough surfaces with h greater than hr; and for h between hs and hr, z0c is interpolated linearly between z0 = czs hs at h = hs and z0 = czr hr at h = hr. The effect of stems and branches is assumed to be included in z0c.
The zero-plane displacement of a closed canopy, dc (DISPC), is generally related to canopy height, h, and to z0c by
(22) dc = h - z0c / 0.3
(Monteith 1973; Shuttleworth and Gurney 1990).
When h (HEIGHT) is small, it is possible for z0c to be less than z0g (Z0GS), which is the parameter giving roughness of the ground surface under the canopy. This impossible situation would cause problems later on. It is prevented by reducing z0g to the value of z0c, which works nicely because z0c is always added to dc.
The values of d and z0 for sparse canopies (RATIO < 1) are obtained by a modification of the method that Choudhury and Monteith (1988) developed from curves of Shaw and Pereira (1982). A drag coefficient per unit leaf area and stem area, cd (CDRAG), is calculated from z0c and dc as
(23) cd = { -1 + exp [ 0.909 - 3.03 ( z0c / h ) ] } 4 / (Lpc + Spc) .
This assumes that a unit of Spc produces the same drag as a unit of Lpc. Then
(24) d = 1.1 h ln { 1 + [ cd ( Lp + Sp ) ] 0.25 }.
Shuttleworth and Gurney (1990) also used this approach, but assumed a constant cd of 0.07, which is not appropriate when z0c / h is not 0.13.
For z0, Shuttleworth and Gurney (1990) chose between a sparse canopy equation and the closed canopy value of 0.3 (h - d), depending on a fixed value of cd Lp. However, that procedure leads to a step change at the transition. The step change is avoided by choosing the minimum of the two z0 values, as
(25) z0 = min { 0.3 ( h - d ), z0g + 0.3 h [ cd ( Lp+ Sp) ] 0.5 }
where z0g is the roughness parameter of the ground surface. When a snowpack is present, the value of z0g is replaced by the parameter Z0S before ROUGH is entered.
The reference height at which weather variables are known, za (ZA), is set to a fixed amount (ZMINH) above h. It thus is assumed to move up and down if h changes through the year.
This routine obtains the canopy surface resistance, rsc, which is the classic canopy resistance in the Penman-Monteith equation, using the Jarvis (1976) expression for the factors that control the individual leaf resistance, r, and its reciprocal the leaf conductance, g.
Confusion arises because r and g may be given on the basis of both total leaf surface area and projected leaf area. To straighten this out, consider that evaporation is the product of leaf conductance, g, in units of m3H2O m-2leaf s-1, and leaf area index, L, in units of m-2leaf m-2ground to give a canopy conductance in m3H2O m-2ground s-1. But the leaf area index can be given for projected leaf area, Lp, or for total leaf area, Lt. Similiarly, the conductance can be for projected leaf area, gp, or for total leaf area, gt. But the total evaporation must be the same, so gp Lp = gt Lt is required. In the literature, gt Lt is commonly used for needle-leaved plants and gp Lp for broadleaved plants. Following Körner et al. (1979) BROOK90 uses gp Lp for all plants. For needles, where gt, or its reciprocal rt, is known, then gp = ρ tp gt = ρtp / rt, where ρtp = Lt / Lp. Note that ρtp can vary from 2 for flat needles to π for cylindrical needles. For broad leaves, the leaf resistance is usually given separately as rb for the abaxial (lower) surface, and rd for the adaxial (upper) surface. Each of these is based on the one-sided area of the leaf or the projected leaf area index, so gp Lp = gb Lp + gd Lp = Lp ( 1 / rb + 1 / rd ). For amphistomatous leaves (stomates on both sides) the simplification gb = gd is often assumed, giving gp Lp = 2 gb. The factor of 2 can easily be confused with ρtp = 2, but they are not the same. For hypostomatous leaves (stomates only on the abaxial side), gd = 0 is often assumed, giving gp Lp = gd Lp. BROOK90 uses only gp, which hereafter is called gl, and is independent of assumptions about how gp was obtained.
Stomates open and close in response to several external and internal variables. Jarvis (1976) proposed that the effects could be considered as multiplicative such that
(26) gl = glmin + fT fD fR fW fC ( glmax - glmin )
where gl is the leaf conductance, glmin is its minimum value (closed stomates), glmax is its maximum value, and fT, fD, fR, fW, and fC are reduction factors, varying between 0 and 1, that account for effects of temperature, vapor pressure deficit, radiation (light), leaf water stress, and atmospheric carbon dioxide concentration, respectively, on stomatal opening. This multiplicative expression has been widely used, though more by default and for simplicity than because of any extensive empirical testing. BROOK90 is not concerned with effects of changing atmospheric CO2 effects, so fC = 1 always.
BROOK90 also always uses fw = 1. The resulting rsc is therefore appropriate to the definition of potential transpiration as occurring when soil water is at field capacity. Reduction of fw below 1 in response to drying soil would allow a direct calculation of actual transpiration using the Penman-Monteith or Shuttleworth-Wallace equations. However, BROOK90 does not do this; it simulates actual transpiration as the lesser of potential transpiration using fw = 1 and a supply rate controlled by the water potential gradient and plant resistance.
Of the remaining three dependencies, the temperature response is the least well-documented. Jarvis (1976) proposed a skewed parabolic response, such that stomatal conductance is reduced both by low and high temperatures. BROOK90 uses a slightly simpler response consisting of an optimum temperature range with fT = 1 and inverted half parabolas to reduce fT to 0 at each end of the range, so
| (27) | fT = 0 | Ta < TL |
| fT = 1 - [ (T1 - Ta) / (T1 - TL) ]2 | TL < Ta < T1 | |
| fT = 1 | T1 < Ta < T2 | |
| fT = 1 - [ (Ta - T2) / (TH - T2) ]2 | T2 < Ta < TH | |
| fT = 0 | Ta > TH |
TL, T1, T2, and TH are all parameters. If T1 = T2, there is no optimum range. If TL = T1 and T2 = TH, fT is a square wave function. The use of mean daily temperature, Ta, here instead of some other temperature like minimum daily temperature is arbitrary. The actual temperature response is probably much more complex than this and involves acclimation.
Stomates are known to partially close in response to greater dryness of the air surrounding the leaf, though the mechanism is unclear. The dryness is expressed best by the vapor pressure difference between the leaf and its surrounding air, but as this is not generally known, the atmospheric vapor pressure deficit above the canopy, Da (VPD), is usually used. The error induced by using Da is certainly not larger than the uncertainty in the magnitude of the vapor deficit response for most species. Jarvis (1976) assumed a linear conductivity response, but Lohammar et al. (1980) suggest a linear resistance response such that
(28) fD = cD / ( cD + Da )
where cD (CVPD) is a constant, which is the Da at which fD = 0.5. This has the advantage of approaching 0 as an asymptote when Da is large.
For fR also, several functional forms have been used. BROOK90 uses the form given by Stewart (1988) in which fR = 1 when solar radiation incident on the leaf, RL, is equal to its nominal maximum value, Rm (1000 W/m2), so
(29) fR = (Rm + R0) RL / [ Rm (R + R0) ]
and R0 is a second parameter. A more convenient parameter than R0 is R.5, defined as the radiation level at which fR = 0.5. Then from (29)
(30) R0 = Rm / [ ( Rm / R.5 ) - 2 ]
For most plants, the value of R.5 is relatively low, around 50 to 100 W/m2. In these expressions, the solar radiation at the leaf is used, whereas the stomatal opening is actually influenced by the photosynthetically active radiation. Use of solar radiation, RL, therefore assumes that the spectral distribution of the radiation does not change with depth into the canopy, which is incorrect (Federer and Tanner 1966, can't resist the opportunity to quote my ancient Ph.D. work here!).
The canopy conductance, gsc, which is the reciprocal of rsc, is the integral of gl over each increment of total leaf area in the canopy , dL' , so
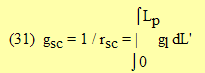
With (26), where fT, fD, and glmax are all assumed constant through the canopy, (31) becomes
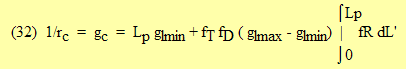
where fR is the only variable that depends on location in the canopy.
Integration of fR requires an expression for the penetration of solar radiation into the canopy. A Beer's Law or exponential extinction is commonly used, such that the average radiation flux density on the leaf surface, RL, at any level in the canopy depends on the projected leaf area, L', and projected stem area, S', above that level, as follows:
(33) RL = CR R exp [ -CR ( L' + S' ) ]
where CR is the
extinction coefficient and R is the solar radiation at the top of the canopy.
The first CR accounts for leaf inclination assuming random azimuthal
distribution (Monteith 1973,
Campbell 1977,
Shuttleworth and Gurney
1990). The S' term was added by
Federer et al. (1996)
and assumes that a unit of projected leaf area and a unit of projected stem
area have the same absorption effect. Assuming that only half of
Sp is distributed proportionally to L' (and the other half is
below the leaves in a "stem space"), then
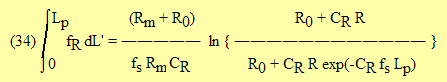
which corresponds to Shuttleworth and Gurney (1990) and Saugier and Katerji (1991) when Sp = 0. The combination of (32) and (34) provides the value of rsc (RSC)
FRSS returns the Shuttleworth-Wallace soil surface resistance, rss (RSS), which must increase with drying of the surface. BROOK90 currently uses only the top soil layer to calculate RSS, no matter what its thickness. The model assumes that the ratio of matric potential (PSIM) to matric potential at field capacity (PSIF) in the surface layer is the controlling variable. Function FRSS is
(36) RSS = RSSA * (PSIM / PSIF) ^ RSSB
where the parameter RSSA is RSS at field capacity, and RSSB is an exponent. The value of RSSA is poorly known; BROOK90 suggests using the Shuttleworth-Wallace value of 500 s/m; soil evaporation (SLVP) will be inversely proportional to this value. Using RSSB = 1 makes SLVP inversely proportional to PSIM in the top layer. Certainly more investigation is required before changing these values for any soil surfaces. A valid relationship is yet to be developed even for bare soil (van de Griend and Owe 1994).
Currently in BROOK90 the presence of intercepted rain (INTR) does not affect RSS. That is, the soil surface is not assumed to be saturated during and after storms. An alternative would be to make RSS = 0 when INTR > 0.
When there is SNOW, RSS is set to zero, which affects calculated transpiration and interception rates, but there is no soil evaporation and snow evaporation is calculated using subroutine SNOVAP. This leaves something to be desired, but the whole situation with melting and evaporating snow as well as transpiration is a complicated mess.
When the parameter RSSA is set to 0 there is no soil evaporation (SLVP).
WEATHER includes all adjustments of input weather data, including separation into daytime and nighttime values.
If daily solar radiation (SOLRAD) is input as zero, it is estimated as 0.55 * I0HDAY, or 55% of the potential solar radiation for the doy and location. The 0.55 value is an overall generalization for the United States, where values range from 0.50 in the east to 0.60 in the west (U.S. Department of Commerce 1968). As of Version 4.8 this value can be changed on the BROOK90 main window.
If vapor pressure (EA) is input as zero, it is estimated as the saturated vapor pressure at the minimum daily temperatire (TMIN) using subroutine ESAT.
If daily average wind speed at a weather station (UW) is input as zero, it is estimated as 3 m s-1. This is a surprisingly good approximation for most weather stations in the United States at all seasons of the year (U.S. Department of Commerce 1968). For other default values, enter the value as UA for each day in the data file. Note: measured values of zero wind speed should be entered as 0.1.
The average temperature for the day (TA) is taken as the average of the input maximum and minimum temperatures (TMAX and TMIN). Daytime (TADTM) and nighttime (TANTM) average temperatures are calculated by assuming a sine wave variation between TMAX and TMIN. Integration leads to
TADTM = TA + [ (TMAX - TMIN) / (2 π DAYLEN) ] sin( π DAYLEN )
TANTM = TA - { (TMAX - TMIN) / [2 π (1 - DAYLEN)] } sin( π DAYLEN )
where DAYLEN is the solar daylength determined in subroutine SUNDS.
For wind speed, a parameter, WNDRAT, defines the average ratio of nighttime wind speed (UANTM) to daytime wind speed (UADTM). The default value for WNDRAT is 0.3 based on Hubbard Brook data.
UADTM = UA / [ DAYLEN + (1 - DAYLEN) WNDRAT ]
UANTM = WNDRAT * UADTM
where UA is the daily average wind speed at height za.
TA, UA, and the vapor pressure, EA, which is assumed constant over the day, are all theoretically the values at the reference height above the canopy (ZA) . In practice, these values are rarely measured above the canopy of interest, but are usually from some relatively nearby weather station. Any attempt to theoretically adjust TA and EA would require some information on their profiles, such as surface temperature and vapor pressure, which are not known. So BROOK90 assumes that TA and EA are the same at the weather station and at za. However, UA can be estimated from wind speed at the weather station (UW) because wind speed extrapolates to zero at height z0 + d over both surfaces. This adjustment is done in function WNDADJ. UW is prevented from being less than 0.2 m s-1.
Subroutine WEATHER could be modified to do further adjustments to temperature, vapor pressure, and wind. For instance, an elevation adjustment to temperature could be added, using the average environmental lapse rate of -0.6°C / 100m.
This function estimates the wind speed (UA) at reference height ZA above the canopy from input wind speed at a remote weather station (UW). Assume that the weather station represents a new surface downwind that has a roughness of z0w (Z0W) and a fetch of F (FETCH). Brutsaert (1982) gives the height of the internal boundary layer, zb, as
zb = 0.334 F0.875 z0w0.125
For logarithmic wind profiles over both surfaces to have the same wind speed at zb,
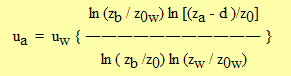
where zw (ZW) is the height of wind measurement at the weather station (Federer et al. 1996) and d (DISP) is the zero-plane displacement of the canopy. This assumes that the weather station is over a smooth surface so its zero plane displacement can be ignored. If the parameter Z0W is set to zero, then no adjustment is made and ua = uw.
![[Compass Brook logo]](cblogo.gif)