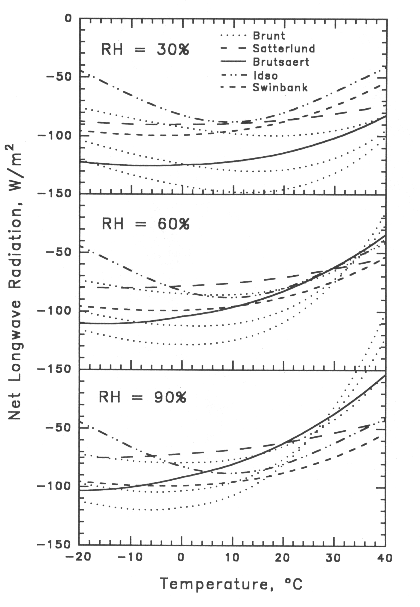
Fig. SUN-1. Net longwave radiation from a clear sky estimated
by five different equations, as a function of temperature for three relative
humidities. The Y axis should read "Net Longwave Radiation from Clear Sky".
EQUIVSLP - SUNDS and FUNC3 - HAFDAY - AVAILEN - Clear Sky Longwave Radiation
October 12, 2017
Daily solar radiation on a horizontal surface (SOLRAD in MJ/m2) is an input variable to BROOK90. This value is sometimes called global radiation to emphasize that it includes both direct or beam radiation from the sun and diffuse radiation from the sky hemisphere. It is directly measured by various types of pyranometers at most research sites and some locations of the National Weather Service. SOLRAD is internally prevented from being larger than 0.99 times the potential insolation (in the absence of an atmosphere), I0HDAY.
If no data are available and input SOLRAD is zero, BROOK90 uses a fixed fraction of the potential solar radiation on a horizontal surface. This fraction had been set at 0.55, but as of Version 4.8 it can be changed on the BROOK90 main window. Use of this generalized fraction loses the effects of day-to-day variation of solar radiation in the model.
Alternatively, there are various simple to complicated methods for estimating SOLRAD from cloud cover measurements, which are more widely made (Brutsaert 1982, Dingman 1994).
Another approach to estimating daily solar radiation uses the fact that the daily temperature range is usually larger on clear days than on overcast ones. The equation of Bristow and Campbell (1984) has been used worldwide in various modifications. For Hubbard Brook I use
R / I0 = a (1 - exp(-b Δ ^ c)) + d
where R is the daily solar radiation, I0 is the potential insolation (I0HDAY), and Δ is the daily temperature range (Tmax - Tmin), and a, b, c, and d are constants that depend more or less on location. I added the d value so that R is greater than zero when Δ is zero. For Hubbard Brook I use a = 0.78, c = 1.5, d = 0.05, and b = 0.245 + 0.0035 sin(2π (doy + 80) / 366) to account for some residual seasonality, where doy is day of the year.
In BROOK90 subroutine EQUIVSLP is called once to obtain parameters that depend on latitude, slope, and aspect of the surface being simulated. Subroutine SUNDS uses functions FUNC3 and HAFDAY once a day to calculate daylength, potential radiation on a horizontal surface, and the ratio of potential radiation on the slope to that on a horizontal surface. AVAILEN calculates net radiation minus soil heat flux at the top and the bottom of the canopy, separately for daytime and for nighttime.
Correction of solar radiation for slope and aspect requires calculation of an "equivalent slope" in subroutine EQUIVSLP. The equivalent slope is defined as the location on the earth's surface where a horizontal surface is parallel to the given sloping surface. Following Swift (1976), L1 is the latitude of this "equivalent slope" (which is actually a horizontal surface), and L2 is the difference in hour angle (longitude) between the two locations. For any given slope and aspect, L1 and L2 need be found only once; they do not change over time. So they are calculated in EQUIVSLP at the beginning of B90, as:
L1 = ASIN[ COS(SLOPE) * SIN(LAT) + SIN(SLOPE) * COS(LAT)* COS(ASPECT) ]
and
L2 = ATAN { SIN(SLOPE) * SIN(ASPECT) /[ COS(SLOPE) * COS(LAT) - SIN(SLOPE) * SIN(LAT) * COS(ASPECT) ] }
with fixes for negative or zero denominator in L2, where SLOPE (ESLOPE), ASPECT, and latitude (LAT) are input parameters describing the location. All angles in the subroutine are in radians.
Several radiation-related variables depend only on day of the year and location. These are calculated in SUNDS, which is called once a day.
SUNDS requires the solar constant (SCD), which is the radiation (W/m2) on a surface normal to the sun outside the atmosphere. It depends on day-of-the-year (DOY) to determine the earth-sun distance and is
SCD = SC / (1 - .0167 * COS(.0172 * (DOY - 3))) ^ 2
where SC is the solar constant at the mean earth-sun distance (Swift 1976). SC is set to 1367 W/m2 (Lean 1991) and can not be changed.
The declination of the sun (DEC) is the angle by which the sun is above or below the plane of the earth's equator. DEC is zero at the equinoxes and +23.5° or -23.5 at the solstices. Swift (1976) gives the solar declination (radians) as:
DEC = ASIN { 0.39785 * SIN [ 4.86961 + 0.017203 * DOY + 0.033446 * SIN ( 6.224111 + 0.017202 * DOY ) ] }
The daily integral of potential insolation on a slope (I0SDAY, MJ/m2) is given by Swift (1976) as:
I0SDAY = WTOMJ * SCD * FUNC3(DEC, L2, L1, T3, T2)
where
FUNC3 = (π/ 2) { SIN(DEC) * SIN(L1) * (T3 - T2) + COS(DEC) * COS(L1) * [ SIN(T3 + L2) - SIN(T2 + L2) ] }
is a program function and T2 and T3 are the hour angles of sunrise and sunset on the slope, which are obtained from function HAFDAY using the latitude of the equivalent slope. FUNC3 has units of d-1 and WTOMJ is the conversion factor 0.0864 (MJ m-2 d-1) / (W m-2). The actual SUNDS algorithm is more complicated than this because it must consider the possibility of two sunrises and sunsets on the slope in one day. The details of the algorithm are given by Swift (1976). Note that this algorithm assumes that the "opposing slope" is horizontal. In reality in mountainous terrain, the potential insolation is further reduced by any distant terrain that obscures the horizon more than the given slope itself does. The calculation of such obscuration is difficult and is outside the scope of BROOK90.
The daily integral of potential insolation on a horizontal surface (I0HDAY, MJ/m2) is found from the I0SDAY equation with L1 = LAT, L2 = 0, and T3 and T2 for a horizontal surface at LAT. The daylength (DAYLEN), which is the fraction of a day that the sun is above a horizontal horizon, is HAFDAY / π where function HAFDAY is used with L = LAT. SLFDAY is the ratio of I0SDAY to I0HDAY. SUNDS outputs DAYLEN, I0HDAY, and SLFDAY.
Daylength is calculated here as half-day length (HAFDAY), which is half the time interval between sunrise and sunset. The half-day length in radians is :
HAFDAY = ACOS[ -TAN(DEC) * TAN(L) ]
where DEC is solar declination and L is either latitude or latitude of the equivalent slope. Function HAFDAY includes fixes for the poles or for the sun continuously above or below the horizon.
Estimates of available energy above and below the canopy are made in subroutine AVAILEN. Available energy is net radiation minus subsurface heat flux (SHEAT), and is the energy available for partitioning into heating the air and evaporating water. SHEAT is set to zero in code in MSBSETVARS.
AVAILEN calculates the available energies on an instantaneous basis, that is, in W/m2. MSBDAYNIGHT supplies to AVAILEN the average daytime solar radiation on the given slope (SLRAD, W/m2) as
SLRAD = SLFDAY * SOLRAD / (WTOMJ * DAYLEN)
where SOLRAD is the input daily solar radiation (MJ m-2) on a horizontal surface, and WTOMJ converts W m-2 to MJ m-2 d-1.
Net solar radiation (SOLNET) is
SOLNET = (1 - ALBEDO) * SLRAD
where ALBEDO is the albedo of the surface (above any canopy). When there is snow on the ground, albedo is the parameter ALBSN, otherwise it is the parameter ALB.
Estimation of net longwave radiation has been the subject of much research. BROOK90 uses Brutsaert's (1982) equation for effective clear sky emissivity (EFFEM)
EFFEM = 1.24 * [ EA * 10 / ( TA + 273.15 ] 1 / 7
where EA is the vapor pressure in kPa, and TA is the air temperature in °C. Alternative formulations for clear sky emissivity generally differ by 30 to 50 W/m2 in net longwave radiation under clear sky for the same temperature and humidity. This is equivalent to 1.1 to 1.8 mm/d of evaporated water, a substantial amount! The differences among equations were not systematic but depended on temperature and humidity (see the next section). Consequently the differences are reduced when totalled over a long time, and are further reduced by cloudiness. The Brutsaert equation is the most central.
A cloud cover correction (CLDCOR) to net longwave radiation has been used widely in the form
CLDCOR = C3 + ( 1 - C3 ) * NOVERN
where NOVERN is the sunshine duration for the day, normally written as n/N, or the fraction of possible hours of sunshine. C3 is a fixed parameter in BROOK90. NOVERN is obtained by inverting a common relation of solar radiation to sunshine duration to the form
NOVERN = ( RATIO - C1 ) / C2 , but not < 0 or > 1,
where RATIO is SOLRAD / I0HDAY, or the ratio of solar radiation to potential radiation on a horizontal surface, and C1 and C2 are empirical parameters.
The net longwave radiation (LNGNET) is
LNGNET = ( EFFEM - 1 ) * CLDCOR * SIGMA * ( TA + 273.15 )4
where SIGMA is the Stefan-Boltzmann constant. Then net radiation (RN) is
RN = SOLNET + LNGNET
and available energy above the canopy (AA) is
AA = RN - SHEAT.
Net radiation is assumed to be reduced exponentially down through the canopy according to an extinction coefficient (CR) and the sum of leaf area index (LAI) and stem area index (SAI), so the available energy at the ground (ASUBS) is
ASUBS = RN * exp [-CR * ( LAI + SAI ) ] - SHEAT.
Applying the extinction coefficient for photosynthetically-active radiation (CR) to net radiation as well is theoretically incorrect. The extinction coefficient for net radiation should be less than for PAR. But given the other uncertainties in both uses of CR there is not much point in differentiating the two values.
A number of equations exist for estimating downward longwave radiation from clear sky, EFFEM, based only on weather station temperature and humidity. I have compared these methods by showing the net longwave radiation (to avoid the fourth power temperature response of the downward flux) as a function of temperature for three different relative humidities. I have not seen such a presentation in the literature, but it seems to show the differences among methods quite well.
Fig. SUN-1. Net longwave radiation from a clear sky estimated
by five different equations, as a function of temperature for three relative
humidities. The Y axis should read "Net Longwave Radiation from Clear Sky".
The methods differ only in how they express EFFEM (e):
| Brunt (1932) | e = ca + cb ea0.5 |
| Satterlund (1979) | e = 1.08 {1 - exp[-(10 ea)K / 2016]} |
| Brutsaert (1982) | e = 1.24 (10 ea / K)1/7 |
| Idso and Jackson (1969) | e = 1 - 0.261 exp(-0.000777 T2) |
| Swinbank (1963) | e = 0.0000092 K2 |
where ea is the vapor pressure in kPa, T is the temperature in °C, and K is the temperature in °K. The (mostly) upper Brunt curve has ca = 0.65, cb = 0.134 (kPa-0.5) (Fitzpatrick and Stern 1966), the middle curve has ca = 0.52, cb = 0.206 (Brunt 1932), and the lower curve has ca = 0.44, cb = 0.253 (Penman 1948). Note that the Swinbank and Idso-Jackson curves have no humidity dependence. Brutsaert (1982) admits that Satterlund's equation matches the data better below freezing, but Satterlund has a very flat temperature response and is the highest method of all for temperatures of 0 to 20°C and humidities above 60%. The Brutsaert method tends to be the most central over the whole range of possible conditions.
At most temperatures, the range of net longwave radiation is about 50 W/m2, which is equivalent to an evaporation of 1.8 mm/d! The choice of method for clear-sky emissivity thus plays a major role in the value of PE estimates when net radiation is estimated. A major effort using worldwide longwave data (not estimates from models!) will be needed to improve this situation. Fortunately, the cloud cover correction, approximate as it is, brings the net longwave closer to zero and helps wash out the emissivity error.
![[Compass Brook logo]](cblogo.gif)